Interacting Gases#
Let’s return to the Hamiltonian of particles - now with interactions,
the partition function can be written as
where
is the partition function of the ideal gas (Eq. (4.73)), and \(\langle\mathcal{O}\rangle^{0}\) denotes the expectation value of \(\mathcal{O}\) computed with the probability distribution of the non-interacting system.
Without interactions, we have
But the “configuration integral”
can’t be exactly computed in general. We need approximations: molecular dynamics(HW), monte carlo (soon), perturbation theory in \(N / V\) (Mayer Cluster expansion, see text), mean field theory, variational approximations (today).
Before diving in, an exactly solvable warmup:
Gas of hard 1D “spheres” (intervals) of “volume” (length) \(a\). (Tonk’s gas)
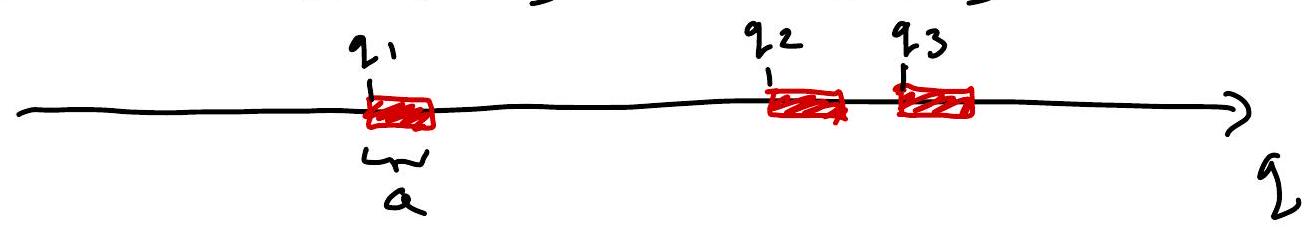
Then
Excluded volume effect#
The “excluded volume” effect extends more generally, but in approximate sense. For this discussion, it is convenient to introduce the excluded volume \(\Omega_{ex}\) of a particle. Consider for example hard spheres of volume \(\Omega\). Then one sphere excludes all other sphere centers from a sphere of twice the radius, or volume \(\Omega_{ex}=2^D\Omega\), i.e. larger than just the sphere itself. Naively, we would then approximate the configurational integral as
This is approximate because of jamming …
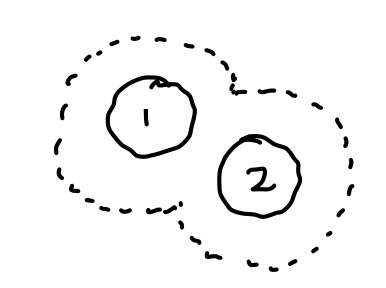
The excluded volume for particle 3 once 1,2 placed is not strictly additive if 1,2 are close: 3 has more space available when 1,2 are close than if they are apart (see depletion force).
But if \(N \Omega_{ex} \ll V\), this interaction is rare, so approximation ok in dilute limit. So,
So effectively \(\quad V \longrightarrow V-N \Omega_{ex}/2\).
Note that this result reproduces our exact result in one dimensions, where \(\Omega_{ex}=2 a\).
This is an example of a “viral expansion”
As explained in the textbook, the \(B_{n}(T)\) can be computed systematically via a diagrammatic perturbation theory. This Mayer Cluster Expansion is however rather technical and its applicability somewhat limited - so we won’t discuss it in class. But have a look, especially if you’re interested in QFT. Here’s we’ll focus on the variational treatment.
Variational treatment of a gas and the van der Waals equation of state#
Our approximate treatment of a hard-sphere gas took only the “excluded volume” repulsion
But neutral molecules interact through an attractive \(U(r) \approx-4 \epsilon\left(\frac{\sigma}{r}\right)^{6}\) as \(r \rightarrow \infty\), with short-range repulsion. Why? The charged constituents of a molecule can polarize:

Since a dipole generates \(E \propto \frac{d}{r^{3}}\), and \(U\propto-\vec{E} \cdot \vec{d}\), i.e.
We can then treat this in quantum perturbation theory for a rotationally-symmetric molecule. In ground state, \(\langle\vec{d}\rangle=0\) so to first order \(\Delta E=0\). If \(\Delta=E_{1}-E_{0}\) is gap, and second order perturbation theory gives
Since \(U \sim \frac{d_{1} d_{2}}{r^{3}}, \quad \Delta E \sim-\frac{1}{r^{6}}\)
The competition between attraction, repulsion, and entropy leads to the presence of complex phase diagrams:
Mean-field treatment#
We will see that the \(Q\)-ensemble is convenient: \(\mu\) is like the “B” of Ising model, while the density \(n=N/V\) jumps like \(m\).
Variational ansatz:#
where \(N\) is our variational parameter.
If we treat the \(\left|r_{i}-r_{j}\right|>r_{0}\) constraint via the low-\(n\) excluded volume approximation,
But in the thermodynamic limit, only one \(N^{\prime}=N=N(\mu, T, V)\) contributes:
We can then apply the Gibbs inequality
Fortunately, is is easy to compute \(\left\langle U\left(r_{i}-r_{j}\right)\right)_{N}\) because in \(\langle\rangle_{N}\) particles are uncorrelated outside \(r_{0}\) :
For \(U(r)=-U_{0}\left(\frac{r_{0}}{r}\right)^{\alpha}\) for example,
So
Simple physical interpretation: each particle sees \(-u \cdot n\) on average from other particles (mean-field)
Note that the LHS has a simple interpretation in terms of pressure:
So, Eq. () can be rewritten as
Thus, our best variational approximation of the true pressure is obtained by maximizing \(\psi\) w.r.t. \(n\),
We’ll see that, as a function of \(n\), \(\psi[n,\mu,T]\) exhibits two maxima corresponding to gas and liquid. Which maximum is the global one depends, for a given temperature \(T\), on \(\mu\). To get a better sense of the behavior of \(\psi_u[n,\mu,T]\), we’ll rescale all parameters in terms of their characteristic values,
Then, our function \(\psi\) becomes
The procedure above is called “Non-Dimensionalizing” and has three benefits.
Note
Non-Dimensionalizing equations
Revealing characteristic scales: Each remaining “tilde” variable is just a number and represents the original variable in units of its characteristic scale: \(\tilde \psi\) measures \(\psi\) in units of the characteristic pressure \(P_0 =2 k_B T/\Omega_{ex}\). Without doing anything further, we know that the problem will depend on how the pressure relates to this characteristic pressure. The density is measured in units of its characteristic density \(2/\Omega_{ex}\), which is the maximal density possible with hard core interactions. etc.
Simplification: the process has uncovered that \(\tilde \psi\) really is just a function of three independent control parameters, \(\tilde u\), \(\tilde mu\) and \(\tilde n\). The parameter temperature could be fully absorbed in one of the other effective parameters.
Plotting: Thirdly, because the remaining formula relates numbers to numbers, we can directly produce plots to get a sense of the behavior of \(\tilde \psi\), without worrying about what units we should put on the different axis: Each effective parameter should be studied for values much smaller and much larger than 1.
Now, let’s maximize \(\tilde \psi\) w.r.t. our variational parameter \(\tilde n\):
This has multiple \(\tilde n\)–solutions for a given \(\tilde \mu\) (see below).
Van der Waals equation of state#
But for a given \(\tilde n\), it has a single \(\tilde \mu\) solution
Substituting this back into our approximation Eq. (), we obtain an approximation of the pressure as a function of density,
Reinserting the original variables, we obtain the well-known Van der Waals equation of state:
We see the two phenomenological coefficients \(a\) and \(b\) of VdW have their origin in the mean field treatment of long-range attraction (a) and short-distance repulsion (b).
In terms of the molecular volume \(v=n^{-1}\), we can also write
showing that effect of long-range interaction is to shift \(P \rightarrow P-a n^2=P-a v^{-2}\) due to the average attraction \(u n\) experienced by each particle (mean-field).
Phase transition#
Let’s return to () determining the optimal density given the chemical potential, which can be rewritten as
Note that the LHS is a complicated non-linear function, but does not depend on any parameter. The RHS is merely a straight line with axis intercept \(-\tilde \mu\) and negative slope \(-\tilde u\). So, we may solve the equation graphically by plotting the parameter-free RHS, and see under which conditions this function can be cut by a negative slope straight line.
Show code cell source
import numpy as np
import matplotlib.pyplot as plt
# Define the first function to plot
def newly_corrected_function(n):
return np.log(n**(-1) - 1) - 1 / (1 - n)
# Define the second function to plot
#def second_function(n, tilde_mu=-1.9, tilde_u=8):
def second_function(n, tilde_mu=-4, tilde_u=13):
return -tilde_mu - tilde_u * n
# Generate a range of tilde n values within the specified interval
n_values_new_interval = np.linspace(0.001, .9, 400)
# Calculate the function values for both functions
newly_corrected_function_values_new_interval = newly_corrected_function(n_values_new_interval)
second_function_values = second_function(n_values_new_interval)
# Plot both functions
plt.figure(figsize=(10, 6))
plt.plot(n_values_new_interval, newly_corrected_function_values_new_interval, label='ln(n^-1 - 1) - 1/(1-n)')
plt.plot(n_values_new_interval, second_function_values, label='-tilde_mu - tilde_u*n', linestyle='--')
plt.title('Comparison of Functions')
plt.xlabel('n')
plt.ylabel('Function Value')
plt.legend()
plt.grid(True)
plt.show()

From the plot above, we can see that we can have three extrema. Plotting \(\psi\) on a log plot shows that there are two maxima and a minimum in the middle. Which maximum dominates, depends on the chemical potential \(\mu\):
Show code cell source
import numpy as np
import matplotlib.pyplot as plt
# Define the updated function with both tilde u and tilde mu parameters
def psi_tilde_updated(n, mu, u):
return n * np.log(n**(-1) - 1) + mu * n + u * (n**2) / 2
# Generate a range of tilde n values within the specified interval
n_values = np.linspace(0.001, .8, 400)
# Specify a range of tilde mu values for plotting
mu_values = [-1.7,-1.8, -1.875, -1.95, -2.1]
# Specify a range of tilde u values for plotting
u_values = [8]
# Plot the function for various combinations of tilde u and tilde mu values
plt.figure(figsize=(8, 6))
for mu in mu_values:
for u in u_values:
plt.plot(n_values, psi_tilde_updated(n_values, mu, u), label=f'$\mu={mu}, u={u}$')
plt.title('Plot of $\~\psi_{\~u}(\~n, \~\mu, \~u)$ as a function of $\~n$')
plt.xlabel('$\~n$')
plt.ylabel('$\~\psi_{\~u}(\~n, \~\mu, \~u)$')
#plt.yscale('log')
plt.legend()
plt.grid(True)
plt.show()
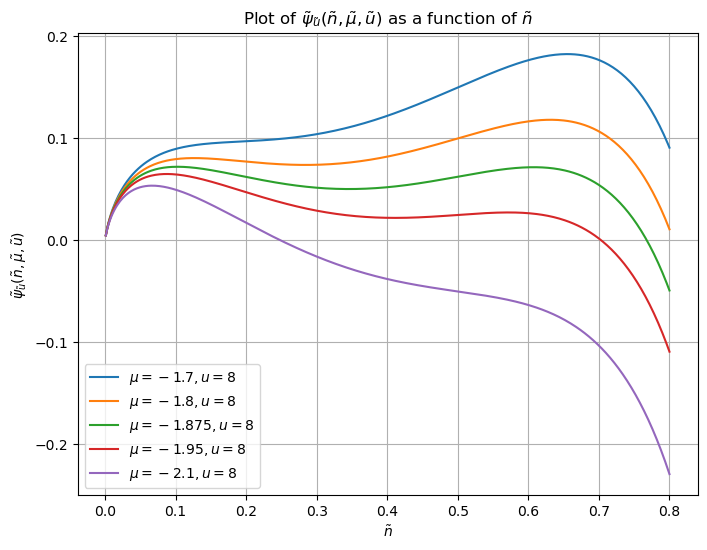
The interpretation here is that for low \(\tilde \mu\) (large negative \(\mu\)), a low density phase obtains, and vice versa for high \(\tilde\mu\). There is a transition point \(\tilde\mu_c(\tilde u)\), where the density jumps – phase transition:

\(\tilde \psi\) has two maxima and one minimum for \(\mu\) near the transition point, indicating that both the low and high-density states are metastable. Once \(\mu\) is still further away from the transition point, the minimum annihilates with one maximum, such that only one maximum remains.
The extremum structure of \(\tilde \psi\) matters for the relaxation to equilibrium. If there are two maxima, and we start out at the lower maximum, relaxation proceeds via droplets of a minimal size. If there’s just one maximum, the relaxation proceeds spontanously.
Minimal attractive interaction#
However, to be able to observe a phase transition as function of \(\mu\), the value of \(\tilde u\) has to exceed a critical \(\tilde u_c\) so that \(\tilde \psi\) has two maxima and one minimum. We can determine the minimal \(\tilde u_c\) by finding the maximal slope of the LHS in (15),
The maximal slope occurs at \(\tilde n_*=1/3\), and so
So, as we vary \(\mu\), we get a sudden jump in density if the attraction if \(\tilde u>u_c\). In light of definition of \(\tilde u\), this means that the attraction is strong enough for a given temperature and \(\Omega_{ex}\) or the temperature is sufficiently low for a given attraction parameter \(u\) and \(\Omega_{ex}\). Since we can normally not change experimentally any aspect of the Hamiltonian (except for external fields), but we can easily tune the temperature, the statement \(T<T_c(u,\Omega_{ex}) \rightarrow\) phase transition is the most significant one.
We can depict the entire phase behavior in a \((\tilde u, \tilde \mu)\) phase diagram
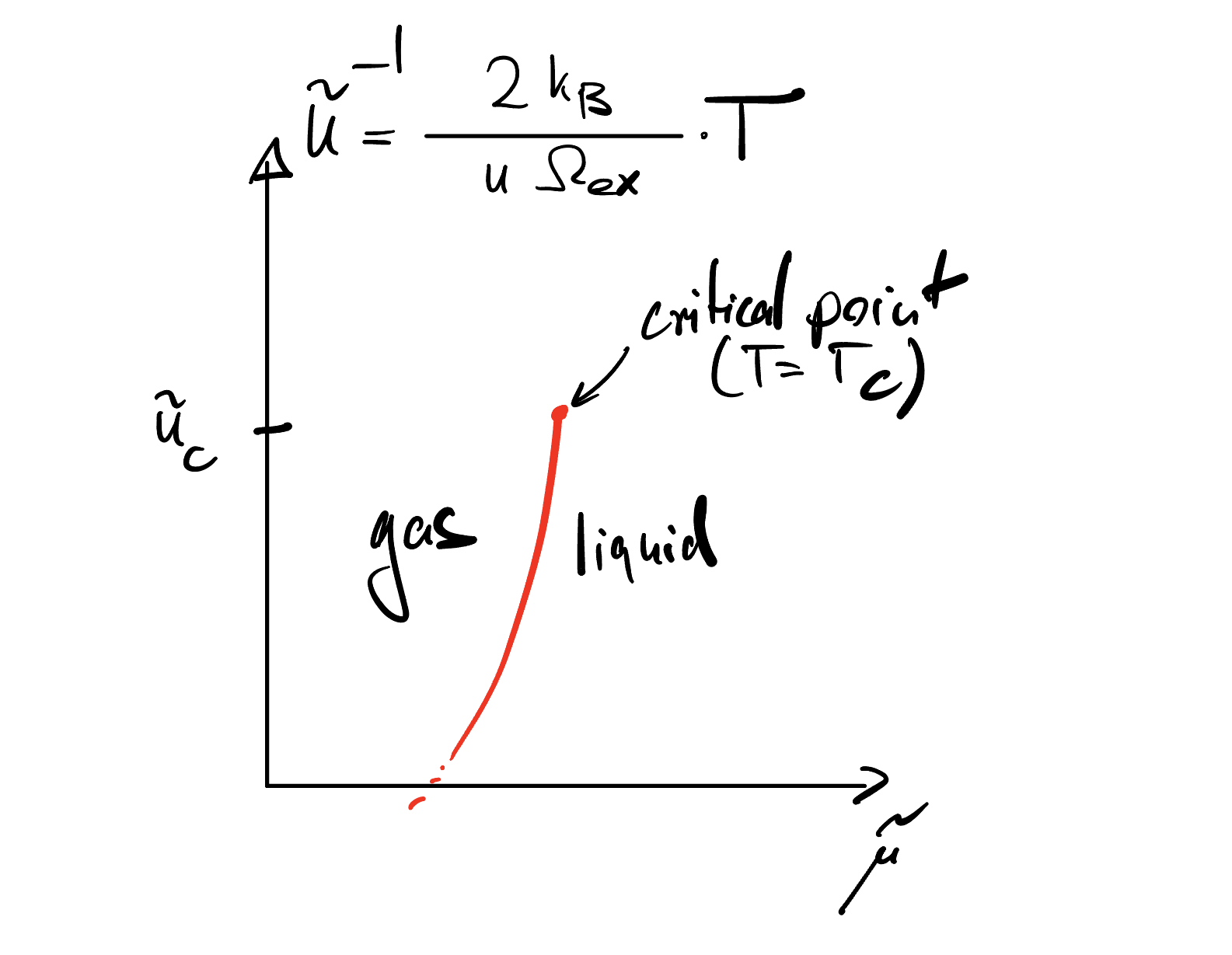
Question: How does the \(\tilde n\) vs \(\tilde \mu\) plot look for \(\tilde u\geq \tilde u_c\)?
Phase separation / Gibbs criterion / Maxwell construction#
If we work in contact with particle reservoir ( \(\mu\)-ensemble), then \(n(\mu)\) jumps below \(T_c\).
But what if we put \(n=\frac{N}{V}\) particles in a box for fixed \(N\) with \(n_{g}<n<n_{l}\) ? Intuitively, we know: it will phase separate:
We can model this situation as two large systems in contact with one another, exchanging particles and volume, and in contact with a joint reservoir, with which they exchange energy:
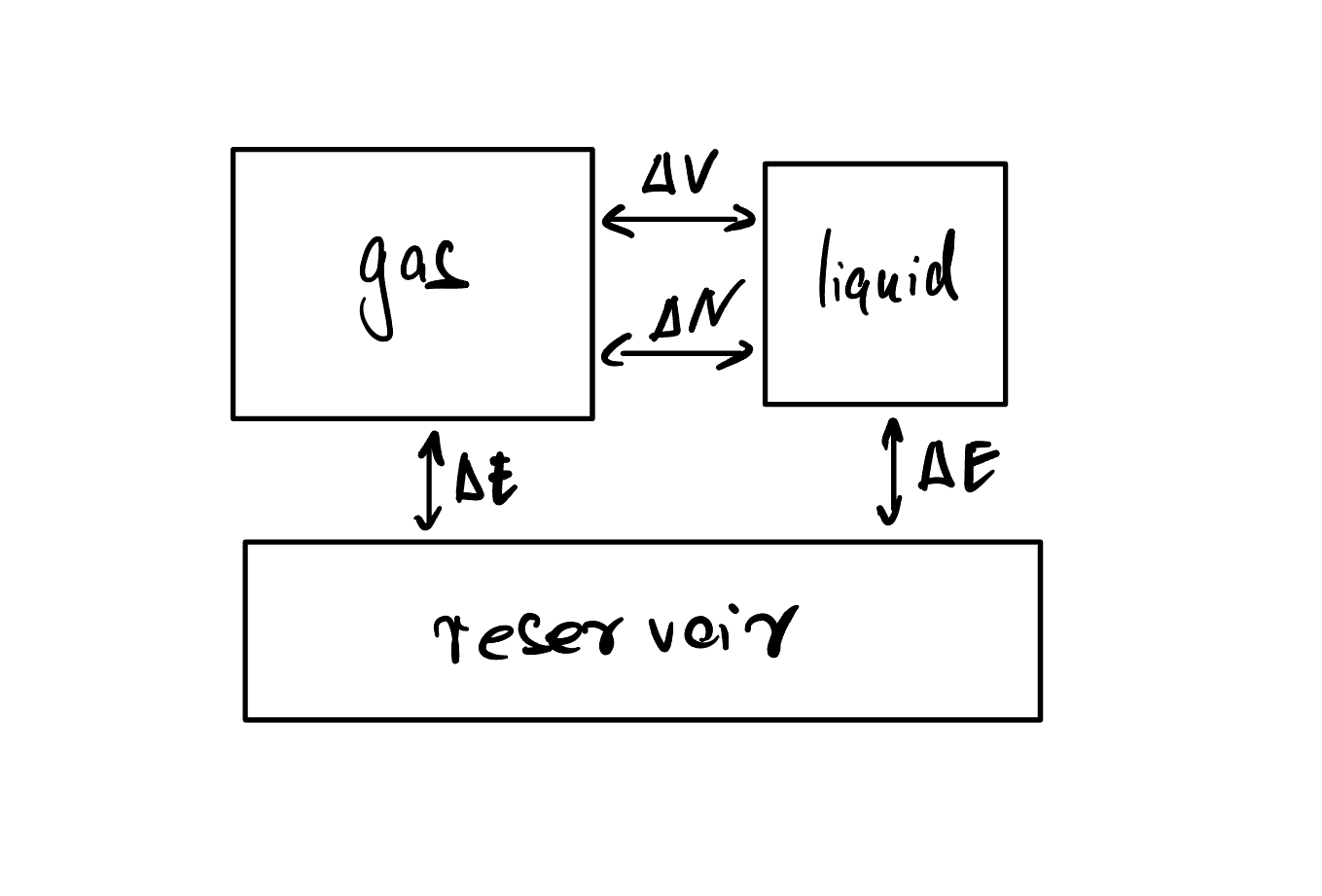
For stability, the liquid and gas compartments need to have the same chemical potential and temperature. I.e. our \(\tilde\psi_{\tilde u}(\tilde n, \tilde\mu)\) function applies to both systems. However, because both systems also exchange volumes, the pressures in both compartments needs to be the same. This restricts the chemical potential to take for a given \(\tilde u<\tilde u_c\) the specific value for which both maxima are at the same height, e.g.
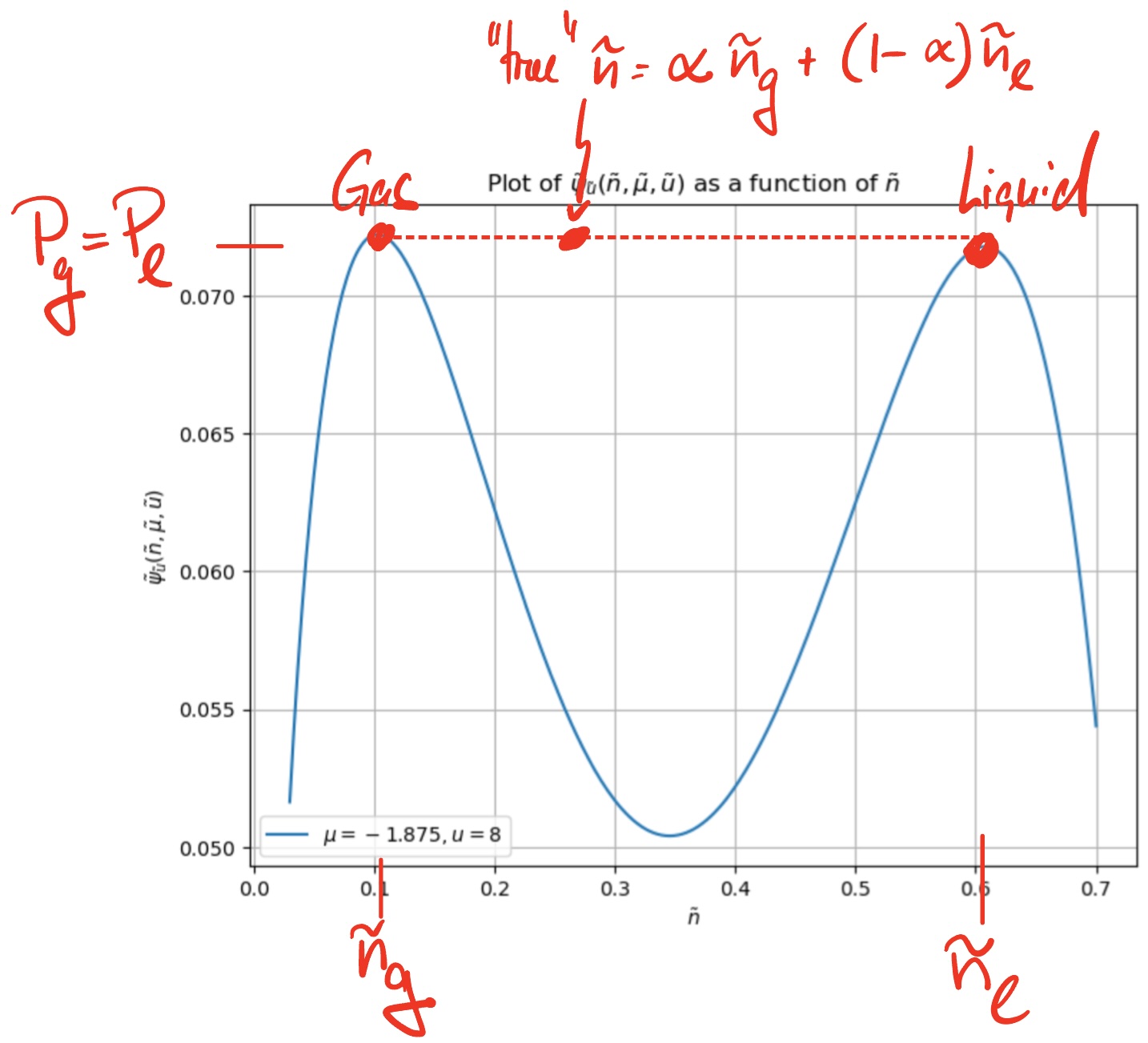
Both maxima determine the pressure in the gas and liquid compartments, and the densities \(n_l > n_g\) determine their volume fraction. If the total density is \(n=N/V\), the liquid volume fraction \(0<\alpha_l<1\) satisfies
Doing this procedure for all possible densities produces the following pressure vs inverse density plot
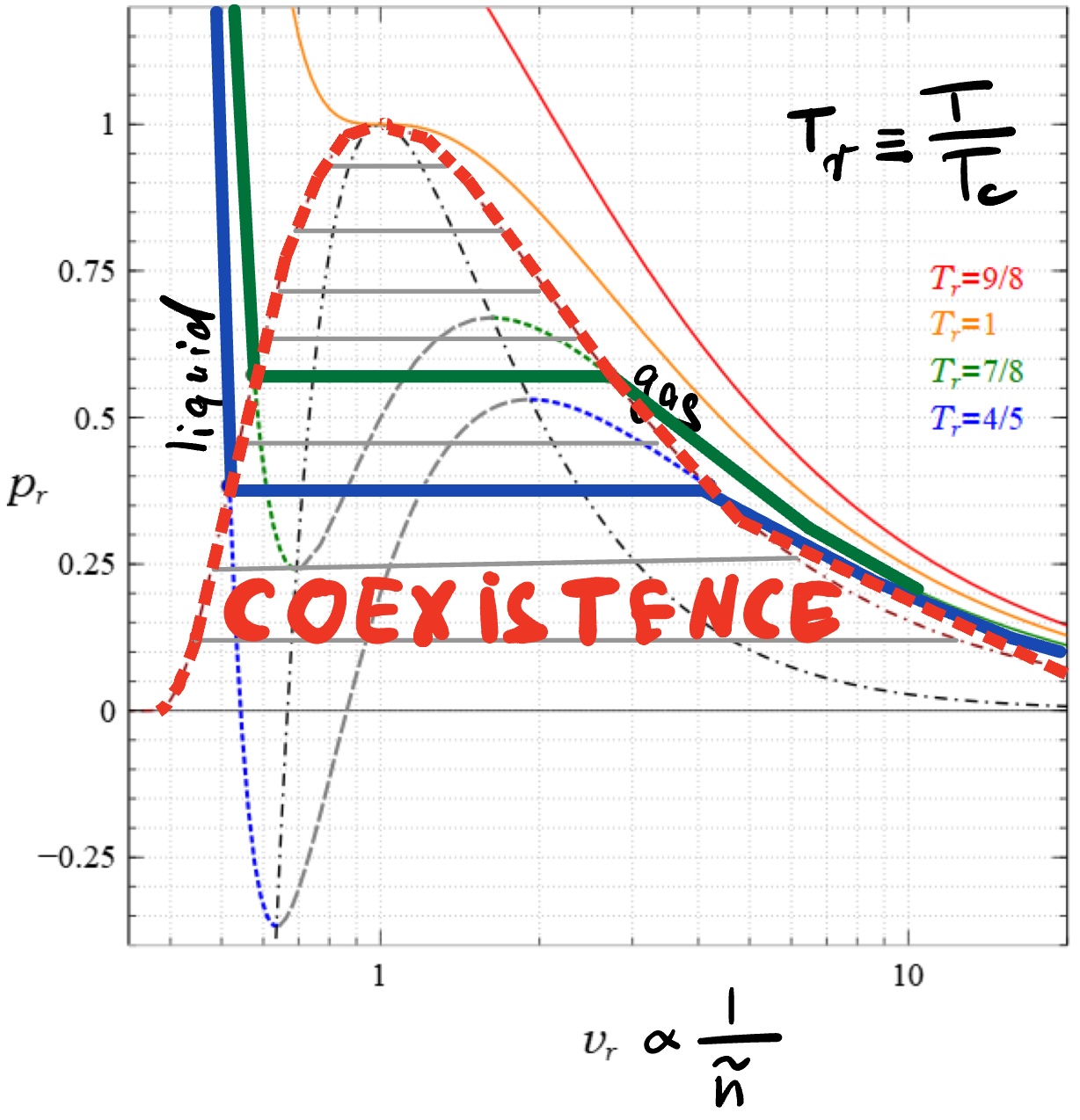
Note that the above approach to phase separation (equal pressures and chemical potentials in gas and liquid compartments) is equivalent to the more popular Maxwell equal area construction.